EXERCISE 12A
(1) Observe the table given below and in each one find whether x and y are proportional:
(i)
| x | 3 | 5 | 8 | 11 | 26 |
| y | 9 | 15 | 24 | 33 | 78 |
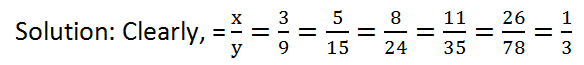
∴ x and y are directly proportional.
(ii)
| x | 2.5 | 4 | 7.5 | 10 | 14 |
| y | 10 | 16 | 30 | 40 | 42 |
Solution: We have:
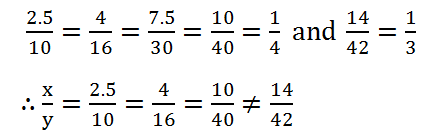
∴ x and y are not directly proportional.
(iii)
| X | 5 | 7 | 9 | 15 | 18 | 25 |
| y | 15 | 21 | 27 | 60 | 72 | 75 |
Solution: We have:

∴ x and y are not directly proportional.
(2) If x and y are directly proportional, find the values of x1, and x2 and y1 in the table given below:
| x | 3 | x1 | x2 | 10 |
| y | 72 | 120 | 192 | y1 |
Solution: Since x and y are directly proportional. We have: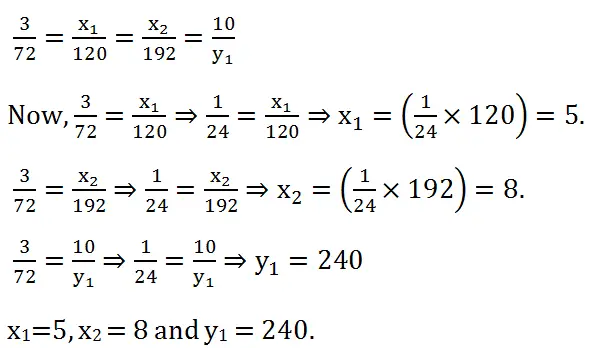
x1=5, x2 = 8 and y1 = 240.
(3) A truck covers a distance of 510 km in 34 litres of diesel. How much distance would it cover in 20 litres of diesel?
Solution: Let the required distance be x km. Then, we have:
| Quantity of petrol(in lit) | 34 | 20 |
| Distance (in km) | 510 | x |
Clearly, less is the quantity of diesel consumed, less is the distance covered. So, it is a case of direct proportion.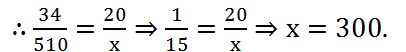
∴ Required distance is 300 km.
(4) A taxi charges a fare of Rs 2550 for a journey of 150 km. How much would it charge for a journey of 124 km?
Solution: Let the required charges be Rs x. Then we have:
| Distance (in Km) | 150 | 124 |
| Charges of fare (in Rs) | 2550 | x |
Clearly, less is the cost, less is the distance of journey.
So, it is a case of direct proportion.
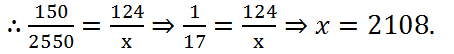
∴ Required amount of charges Rs 2108.
(5) A loaded truck covers 16 km in 25 minutes. At the same speed, how far can it travel in 5 hours?
Solution: Here, 5 hours = (5×60) = 300 minutes
Let the required distance be x km. Then, we have:
| Distance (in Km) | 16 | x |
| Time (in minutes) | 25 | 300 |
Clearly, more distance will be covered more time.
So, it is a case of direct proportion.
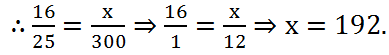
∴ Required distance is 192 Km.
(6) If 18 dolls cost Rs 630, how many dolls can be bought for Rs 455?
Solution: Let the number required dolls be x. Then, we have:
| Number of dolls | 18 | x |
| Cost of dolls (Rs) | 630 | 455 |
Clearly, more dolls will be more cost. So it is case of direct proportion.
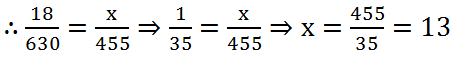
(7) If 9 kg of sugar costs Rs 238.50, how much sugar can be bought for Rs 371?
Solution: Let the required quantity of sugar be x kg. Then, we have:
| Quantity of sugar (in kg) | 9 | x |
| Cost of sugar (in Rs) | 238.50 | 371 |
Clearly, more sugar will be more cost. So it is case of direct proportion.
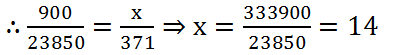
∴ The required quantity of sugar is 14 kg.
(8) The cost of 15 metres of a cloth is Rs 981. What length of this cloth can be purchased for Rs 1308?
Solution: Let the length of required cloth be x metres. Then, we have:
| Length of the cloth (in metre) | 15 | x |
| Cost of cloth (in Rs) | 981 | 1308 |
Clearly, more cloth will be more cost. So it is case of direct proportion.
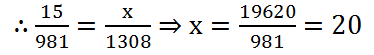
∴ The required length of the cloth is 20 metres.
(9) In a model of a ship, the mast is 9 cm high, while the mast of the actual ship is 15 m high. If the length of the ship is 35 metres, how long is the model ship?
Solution: Let the length of the model ship be x cm.
Here, 15m = 1500 cm and 35 m = 3500 cm
| Length of model ship(cm) | 9 | x |
| Length of actual ship (cm) | 1500 | 3500 |

∴ The required length of the model ship is 21 cm.
(10) In 8 days, the earth picks up (6.4×107) kg of dust from the atmosphere. How much dust will it pick up in 15 days?
Solution: Let the required amount of dust be x kg.
| Time (Days) | 8 | 15 |
| Amount of dust (in Kg) | 6.4×107 | x |
More days will be more dust. So, it is a case of direct proportion.
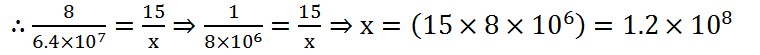
∴ The required amount of dust is 1.2 × 108.
(11) A car is travelling at the average speed of 50 km/hr. How much distance would it travel in 1 hour 12 minutes?
Solution: Let the required distance be x km.
Here, 1 hour 12 minutes = 72 minutes
| Time (In minutes) | 60 | 72 |
| Distance (In Km) | 50 | x |
More time will be more distance. So, it is case of direct proportion.
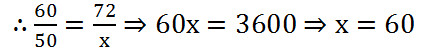
∴ The required distance is 60 km.
(12) Ravi walks at the uniform rate of 5 km/hr. What distance would he cover in 2 hours 24 minutes?
Solution: Let the required distance will be x km.
Here, 2 hours 24 minutes = 144 minutes
| Distance (in Km) | 5 | x |
| Time (minutes) | 60 | 144 |
More time will be more distance. So, it is case of direct proportion.
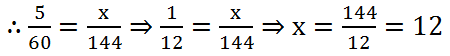
∴ The required distance is 12 km.
(13) If the thickness of a pile of 12 cardboards is 65 mm, find the thickness of a pile of 312 such cardboards.
Solution: Let the thickness of pile be x mm.
| Thickness of pile (in mm) | 65 | x |
| Number of card boards | 12 | 312 |
More cardboard will be more thickness. So, it is case of direct proportion.
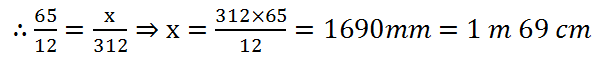
(14) 11 men can dig 6(3/4) metre long trench in one day. How many men should be employed for digging 27 metre long trench of the same type in one day?

∴ The required number of men is 44.
(15) Reenu types 540 words during half an hour. How many words would she type in 8 minutes?
Solution: Here, half an hour = 30 minutes
Let the number of words be x.
| Time (in minutes) | 30 | 8 |
| Number of words | 540 | x |
Less time will be she type Less words. So, it is case of direct proportion.
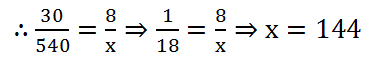
∴ The required number of words is 144.











No comments:
Post a Comment